CWT in PCSEL

old version here

Introduction of Coupled-Wave Theory

Photonic crystal surface-emitting lasers (PCSELs) can realize  one-chip, ultra-large-area, coherent semiconductor lasers. However, it is difficult to accurately evaluate the characterization of PCSELs by traditional simulation method such as FDTD or FEM etc. because of ultra-large computation. Thus, the coupled-wave theory (CWT), which is a semi-analytic computational method, is proposed by research group of Susumu Noda from Kyoto University.
The coupled-wave theory in PCSELs traces its history back to 2006 ^[1], and is expanded to three dimension by incorporating the surface emission and high-order coupling effects^[2]. 3D-CWT has been fully explained in the doctoral thesis of Yong LIANG^[3] and been redefined the coupled matrix by Takuya Inoue^[4].
In this post, I have changed the symbols of some formulas to avoid conflicts.

Bloch’s theorem

Bloch’s theorem^[5] indicates that a periodic potential can be expressed as plane waves modulated by periodic functions.

$$\psi = \mathrm{e}^{\mathrm{i}\vec{k}\cdot\vec{r}}u(\vec{r})$$

where $\vec{r}$ is position, $\psi$ is the wave function, $u$ is a periodic function with the same periodicity as the crystal, the wave vector $\vec{k}$ is the crystal momentum vector, $\mathrm{e}$ is Euler’s number, and $\mathrm{i}$ is the imaginary unit.

Coupled-Wave Theory

2D CWT

Consider a square-lattice of circular holes in the $x$ − $y$ plane with lattice constant $a$, the reciprocal lattice vectors $\vec{G}_{m,n}$ are given by

$$\vec{G}_{m,n} = (m\beta_0,n\beta_0), \tag{1.1}$$

where $β_0 = 2π/a$, and $m$ and $n$ are arbitrary integers. For transverse-electric (TE) mode in square lattice, the magnetic field satisfy the following scalar wave equation

$$\frac{\partial}{\partial x}\left( \frac{1}{k^2}\frac{\partial{H_z}}{\partial x} \right) + \frac{\partial}{\partial y}\left( \frac{1}{k^2}\frac{\partial{H_z}}{\partial y} \right) + H_z = 0 \tag{1.2}$$

where $k^2$ is given by

$$k^2 = \frac{\omega ^2}{c^2}\epsilon (\vec{r}) + \mathrm{i}\frac{2\pi\epsilon_0^{1/2}}{\lambda}\alpha \tag{1.3}$$

where $\omega$ is the angular frequency. $\lambda$ $(c)$ is the wavelength (the speed of light) in the free space. $\epsilon_0$ is the averaged dielectric constant and $\alpha$ is the averaged gain constant.
In a 2D periodic structure, we can apply Bloch’s theory to $(1.2), (1.3)$ and $\epsilon(\vec{r})$, and then we have

$$H_z=\sum_{m,n}H_{m,n}(z)\mathrm{e}^{-\mathrm{i}m\beta_0 x-\mathrm{i}n\beta_0 y}, \tag{1.4}$$

$$\epsilon(\vec{r}) = \epsilon_0^2+\sum_{m,n\neq0}\xi_{m,n}(z)\mathrm{e}^{-\mathrm{i}m\beta_0 x-\mathrm{i}n\beta_0 y}. \tag{1.5}$$

Then, we have

$$\frac{1}{k^2} \approx \frac{1}{\beta^4}\beta^2 - \mathrm{i}2\alpha\beta + 2\beta\sum_{m,n\neq0}\kappa_{m,n}\mathrm{e}^{-\mathrm{i}m\beta_0 x-\mathrm{i}n\beta_0 y}, \tag{1.6}$$

where the coupling coefficient is defined by

$$\kappa_{m,n} = -\frac{\pi}{\lambda\epsilon_0^{1/2}}\xi_{m,n} - \mathrm{i}\frac{\alpha}{2}. \tag{1.7}$$

对于$(1.4)$只考虑四个basic waves也就是$\left|\vec{G}_{m,n}\right|=\beta_0$ 和四个 high-order waves也就是$\left|\vec{G}_{m,n}\right|=\sqrt{2}\beta_0$，那么$H_z$可以简化为

$$H_z(\vec{r})=R_x\mathrm{e}^{-\mathrm{i}\beta_0 x}+S_x\mathrm{e}^{\mathrm{i}\beta_0 x}+R_y\mathrm{e}^{-\mathrm{i}\beta_0 y}+S_y\mathrm{e}^{\mathrm{i}\beta_0 y}+F_1\mathrm{e}^{\mathrm{i}\beta_0 x+\mathrm{i}\beta_0 y}+F_2\mathrm{e}^{-\mathrm{i}\beta_0 x+\mathrm{i}\beta_0 y}+F_3\mathrm{e}^{\mathrm{i}\beta_0 x-\mathrm{i}\beta_0 y}+F_4\mathrm{e}^{-\mathrm{i}\beta_0 x-\mathrm{i}\beta_0 y} \tag{1.8}$$

联立$(1.6)-(1.8)$可得关于四个basic waves的方程

$$(\delta+\mathrm{i}\alpha)R_x = \left( -\frac{4\kappa_1^2}{\beta_0}+\mathrm{i}\kappa_0 \right)R_x+ (-\kappa_3-\mathrm{i}\kappa_0)S_x- \frac{2\kappa_1^2}{\beta_0}R_y- \frac{2\kappa_1^2}{\beta_0}S_y+\mathrm{i}\frac{\partial}{\partial x}R_x , \tag{1.9a}$$

这里的$\kappa_1,\kappa_3,\kappa_0$定义如下，

$$\kappa_1=\kappa_{m,n}|_{m,n\in\{ (1,0),(-1,0),(0,1),(0,-1) \}} \tag{1.10a}$$

$$\kappa_3=\kappa_{m,n}|_{m,n\in\{ (2,0),(-2,0),(0,2),(0,-2) \}} \tag{1.10b}$$

$$\kappa_0=A_0\kappa_1^2 \tag{1.10c}$$

3D CWT

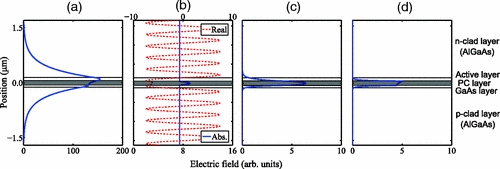
However, distributions of high order waves is different from basic waves. As shown in following figure, high order waves are more concentrated in active layer. It is necessary to consider vertical structure of waveguide layer.

image.png

---

1. Coupled-wave model for square-lattice two-dimensional photonic crystal with transverse-electric-like mode | Applied Physics Letters | AIP Publishing ↩︎

2. Three-dimensional coupled-wave model for square-lattice photonic crystal lasers with transverse electric polarization: A general approach ↩︎

3. Phys. Rev. B 84, 195119 (2011) - Three-dimensional coupled-wave model for square-lattice photonic crystal lasers with transverse electric polarization: A general approach (aps.org) ↩︎

4. General recipe to realize photonic-crystal surface-emitting lasers with 100-W-to-1-kW single-mode operation | Nature Communications ↩︎

5. Bloch’s theorem - Wikipedia ↩︎