Principle of Laser Devices

Introduction of Laser

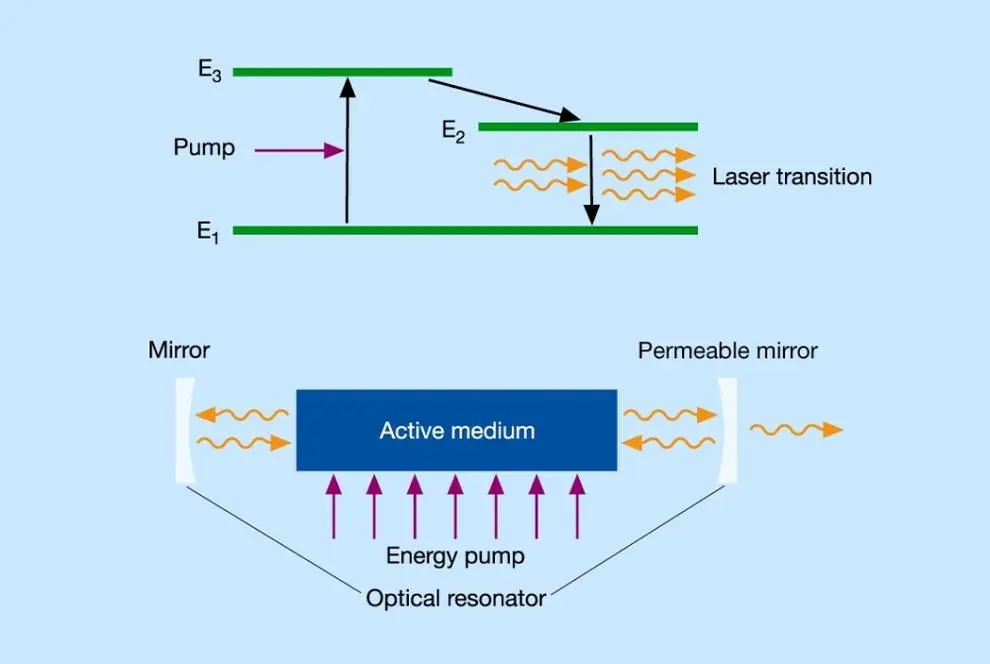
This figure shows principle of a conventional quantum laser where the electrons are bound to atomic, molecular or solid-state energy levels (”bound-electron laser”). Here, laser (active/gain) medium is pumped (by light or electron) and produces spontaneous emission and finally meet “gain” condition (threshold). The semiconductor laser is similar to this.

Threshold condition

To generate laser, it is important to give enough pump power and we can evaluate pump intensity by gain:

$$g = g_0\ln (J/J_0)$$

Where $J$ is current density.
Part of the photons will diffuse to the non-active regions at both ends of the junction, and the lateral spatial distribution of light intensity (photon density) is shown in the figure below:

Photon density in diode

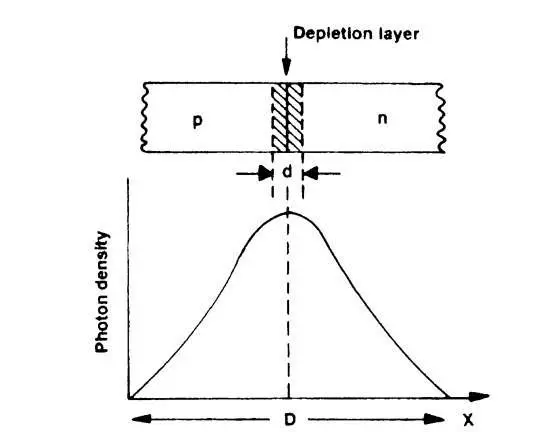
Compared to gain, loss ($\alpha$) describes the optical loss of the cavity. In general, $\alpha$ can be divided into many parts:

$$\alpha = \alpha_{i} + \alpha_{rad} + \alpha_{o}$$

Where $\alpha_{i}$ is internal loss ( mainly due to free carrier absorption of the waveguide material and to scattering loss caused by the roughness of the waveguide wall), $\alpha_{rad}$ is the radiation loss, $\alpha_{o}$ is other loss (in normal negligible).
Once $g \gt \alpha$, pump intensity is enough to laser. Especially, in photonic-crystal surface-emitting lasers (PCSELs), $\alpha$ can be expressed by quality factor ($Q$):

$$\alpha = \frac{2\pi / a}{Q}$$

Where $a$ is period of photonic crystal. And physic define of $Q$ is:

$$Q = 2\pi \nu \frac{E}{P} = 2\pi \nu \tau_R = \frac{\lambda}{\Delta\lambda}$$

Where $E$ is energy in cavity, $P$ is power loss of cavity, $\tau_R$ is called as resonator life, $\Delta\lambda$ is also linewidth (but in wavelength).
Note that only $d/D$ ($\Gamma$, Optical confinement factor) part of the photons are in the active region and generate new photons by stimulated emission. This effect reduces the effective gain of the device. Thus, the threshold condition is:

$$g\Gamma_{QW} = \alpha = \alpha_i + \alpha_{cavity}$$

$$J_{th} = J_0\exp (\frac{\alpha_i + \alpha_{cavity}}{\Gamma_{QW}g_0})$$

In Watt-class high-power, high-beam-quality photonic-crystal lasers | Nature Photonics by S. Noda, the $\lambda$ is 0.94 $\mu m$, $\eta_i$ is 0.9 and $\alpha_i$ is 5 $cm^{-1}$.

Output Power

Obviously, power loss of cavity $E$ can be considered as output power to a certain extent. And all losses are in $\alpha$. Under threshold condition, internal power efficiency is:

$$\eta = \frac{\alpha_{rad}}{\alpha}$$

Differential output power is:

$$\mathrm{d} P_{out} = \eta P_{in} = \eta \left[\frac{\mathrm{d} J}{e} \eta_{i}Sh\nu \right]$$

Where $S$ is area of pump, $J$ is more than the threshold current density $J_{th}$.
Thus, device output power efficiency is:

$$\eta_{out} = \frac{P_{out}}{P_{in}+\left(JS\right)^2 R_s}$$

Where $R_s$ is diode series resistance.
Especially, for PCSELs, only surface emitting laser is under consider. Thus, power efficiency is:

$$\eta=\frac{\alpha_{\perp}}{\alpha_{total}}=\frac{Q_{total}}{Q_{\perp}}$$