Enhancement of PCSEL performance with filling factor and etching depth tuning

Introduction

The photonic crystal surface emitting laser (PCSEL), which has circular beam patterns, low divergence angles, high output power, and single-mode operation, is a novel architecture of semiconductor lasers. Recently, a PCSEL based on GaAs has achieved over 50W single-mode output under CW condition^[1]. PCSEL has also been widely demonstrated with different III/V materials such as InP^[2], GaN^[3], GaSb^[4].
The systematic design theory for PCSEL has been proposed^[5], such as coupled wave theory^[6] (CWT). Different designs of PCSEL lattices can lead to different properties. Circular holes with square lattice gives rise to symmetry protected BIC^[7], while the double lattice enables large scale single mode operation. However, one-dimensional resonant modes with linear far-field appear in some reports for PCSEL.^[8][9][10]. There has not been a well-established explanation for this phenomenon.
In this paper, we design various epitaxial structures for PCSEL and calculate the optical overlap factors of 1D and 2D modes in photonic crystal (PhC) layer and quantum well (QW) layer. The result shows that the filling factor ($FF$) of PhC has a significant effect on optical overlap factors. Based on specific designs, 1D mode can achieve higher overlap in PhC which means stronger in-plane feedback therefore consuming most of the spatial gain required by 2D modes. Therefore, the 2D mode is suppressed. We fabricated PCSEL devices with corresponding epitaxy, and the test results demonstrate the competition between 1D and 2D modes. Further, we optimize the epitaxy design to improve the overlap of 2D modes and thus make 2D mode A become dominant laser mode.

Characteristics of 1D and 2D Modes in PCSEL

The far field pattern (FFP) can be used for distinguishing 1D mode from 2D mode. As shown in Fig 1, FFP of 2D mode is what we usually consider to be PCSEL laser modes. And the 1D mode which is double-lobed longitudinal modes(Fig 1d) is a typical laser mode of surface-emitting DFB lasers^[11]. Two orthogonal 1D modes are presented as shown in Fig 1b, which we call the cross mode. Unlike surface-emitting DFB lasers, the center of the cross mode is dark, which is due to the symmetry-protected far-field cancellation of the BIC resulting from the PhC design.

FIG. 1. (a) 2D mode, (b) orthogonal two 1D modes, (c) 2D and 1D modes appear simultaneously, (d) single 1D mode appeared in PCSEL.

The Theory Model of 1D Mode in PCSEL

For the 2D mode in PCSEL, the theoretical model is well developed. Therefore only the model for the 1D mode is presented here.
Consider transverse electric (TE) polarization in PCSEL, assuming that 1D mode propagates in the $x$-direction, then its amplitude in the y-direction can be approximated as constant. From the Helmholtz equation we can derive the following equation,

$$\nabla^2\vec{E}(\vec{r}) = k_0^2 \epsilon (\vec{r})\vec{E}(\vec{r}) ,\tag{1}$$

where $\vec{E}$is electric field, $k_0$ is free-space wave vector, $\epsilon$ is complex dielectric constant and $\vec{r}$is position vector.
In order to deal effectively with the one-dimensional resonance problem we need to perform a dimensional reduction of Eq. 1. Given that $\frac{ \partial E_{y} }{ \partial y }\approx0$, $E_{x}=0$ and $E_{z}=0$, it is easy to obtain by derivation that

$$\left( \frac{ \partial^{2} }{ \partial x^{2} } + \frac{ \partial^{2} }{ \partial z^{2} } \right)E_{y}(x,z) = k_{0}^2 E_{y}(x,z) \frac{ \int_{0}^{a}\epsilon(x,y,z) \, dy} {a}. \tag{2}$$

Where $a$ is the period on $y$-direction of PhC.

FIG. 2. The 1D Mode in PCSEL (Top View). The arrows indicate the electric field and color indicates its magnitude.

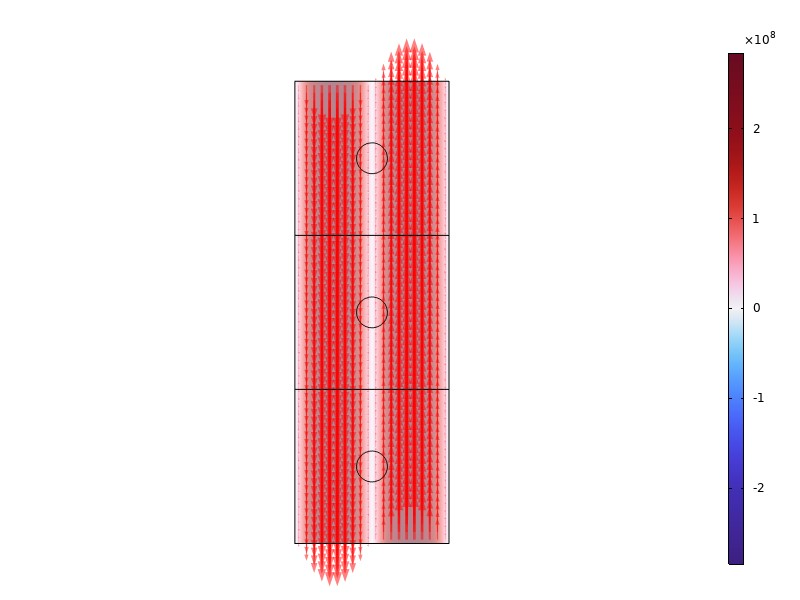
The Simulation of PCSEL Performance

To calculate the properties of PCSEL, we use the finite element method (FEM) to calculate the mode distribution of PCSEL’s unit cell. We calculated the optical overlap factors with PhC and quantum well (QW) $\Gamma_{PhC}$ and $\Gamma_{QW}$ and the radiation constant in vertical direction $\alpha_{\perp}$, defined as follows,

$$\Gamma_{PhC} = \frac{\int _{PhC} |E|^2 \, dV}{\int _{cavity}|E|^2 \, dV } ,\tag{3}$$

$$\Gamma_{QW} = \frac{\int _{QW} |E|^2 \, dV}{\int _{cavity}|E|^2 \, dV } ,\tag{4}$$

$$\alpha_{\perp} = \frac{2\pi}{Q_{\perp}{a}} ,\tag{5}$$

We use FEM to obtain the above performance parameters. The lattice of PhC is defined as Fig 3a shows, the square-lattice with circular air hole is chosen as the PhC for 2D modes. As for 1D modes, we can use effective refractive index ($n_{eff}(x,z)=\frac{ \int_{0}^{a}\epsilon(x,y,z) \, dy} {a}$) obtained from Eq. 2 to describe the model.

FIG. 3. The lattice of PhC is square-lattice and circular air hole which has lattice constant of 298 nm.

FIG. 4. Normalized mode frequency (a), perpendicular Q factor (b), $\Gamma_{QW}$ (c), and $\Gamma_(PhC)$ as a function of FF at different etching depth.

TABLE I. The layer structure of PCSEL for simulation.

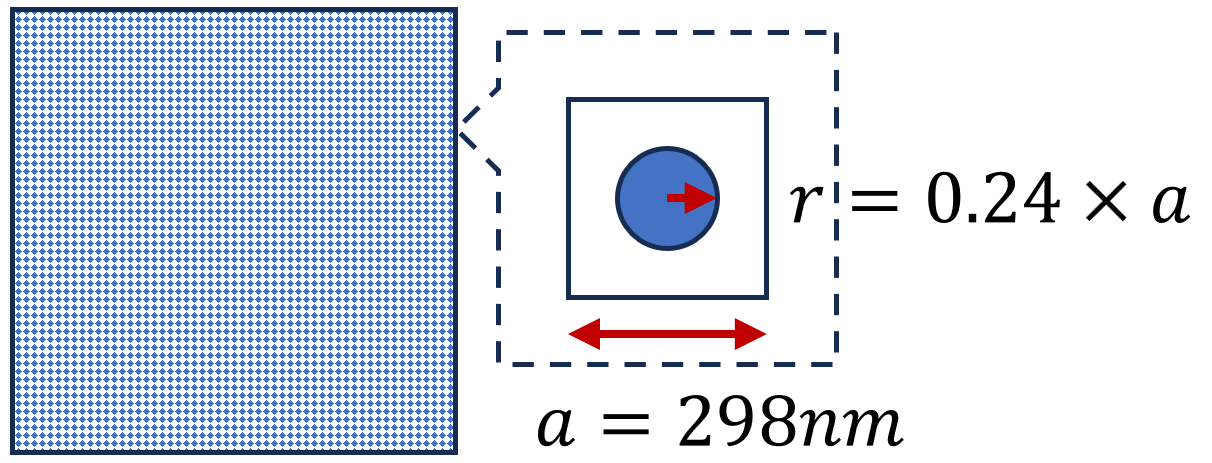
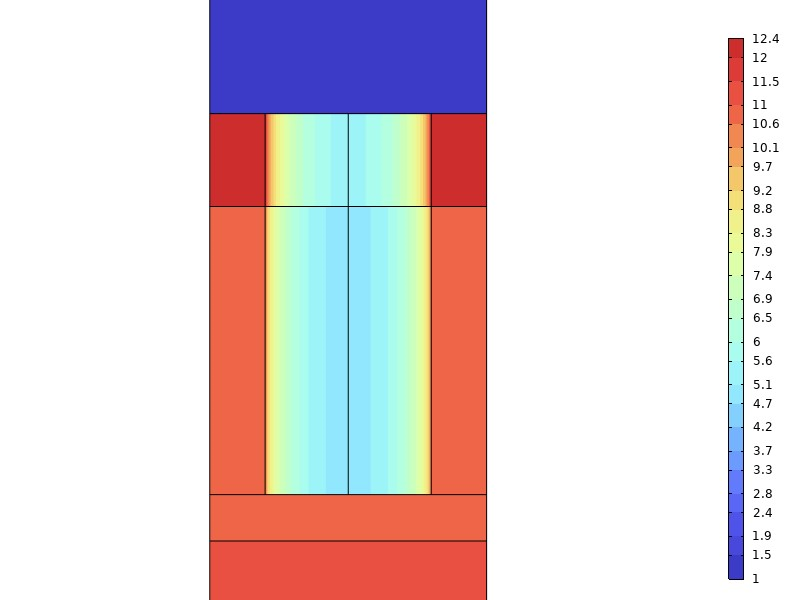
Layer	n	Thickness ($nm$)
Air	1
GaAs	3.4824	100
Al0.4Ga0.6As	3.2744	360
Active Layer		216
Al0.4Ga0.6As	3.2744	2000
GaAs	3.4824

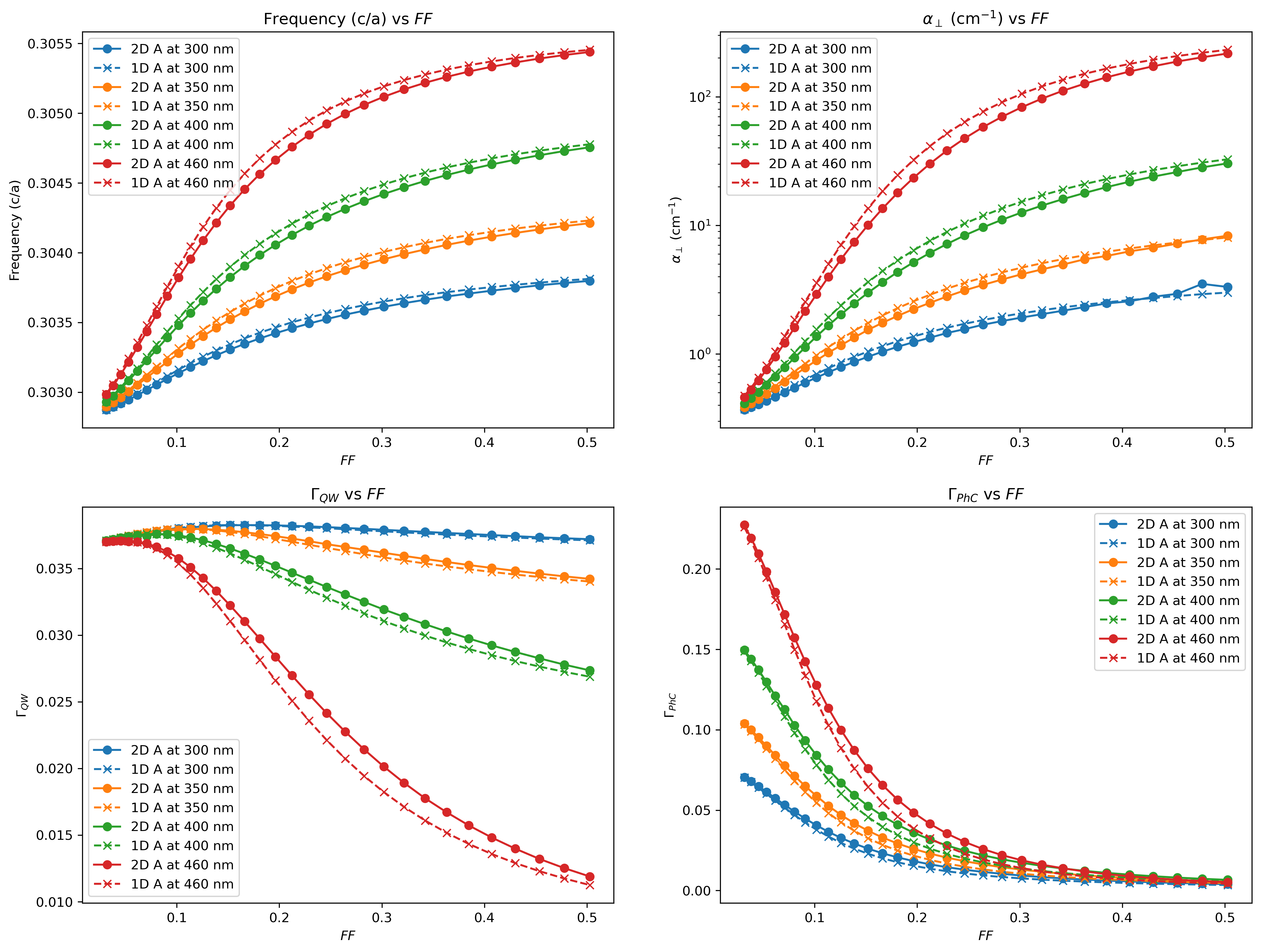
Consider the 2D mode A and 1D mode A which have the highest Q factor in 2D or 1D resonance and thus normally are laser mode. Our simulation results show that the 1D mode A (named 1D A) is extremely close to the 2D mode A (named 2D A) frequency, $\Gamma_{QW}$, $Q_{\perp}$, and $\Gamma_{PhC}$.

Experimental Results

We prepared devices with different etching depths and $FF$, and tested their FFP and calculated PIB (power in the bucket). PIB is used to characterise the energy concentration of the beam and it has the following expression,

$$PIB = \frac{\int _{-r}^{r} \int _{-r}^{r} |E|^2 \, dx\, dy }{\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} |E|^2 dx\, dy } ,\tag{6}$$

Comparing the PIB, we can distinguish two modes. Here we define the radius of the spot with the best 2D unimodality as the radius of the bucket and normalise its PIB to unity, yielding the results shown in Fig. 5.

FIG. 5. The normalized PIB of PCSELs device with different etching depths and $FF$.

Conclusion

Since the generation of 1D mode in PCSEL cannot be explained completely using traditional methods, we believe that this research work has important reference value for the mode selection of PCSEL. This work reveals the competition phenomenon between 1D mode and 2D mode of PCSEL and its causes, which is rarely mentioned in more than 20 years of research on PCSEL.

---

1. High-brightness scalable continuous-wave single-mode photonic-crystal laser | Nature ↩︎

2. 1.5 μm Epitaxially Regrown Photonic Crystal Surface Emitting Laser Diode | IEEE Journals & Magazine | IEEE Xplore ↩︎

3. Green-wavelength GaN-based photonic-crystal surface-emitting lasers - IOPscience ↩︎

4. Continuous wave room temperature operation of the 2 μm GaSb-based photonic crystal surface emitting diode lasers | Applied Physics Letters | AIP Publishing ↩︎

5. High-power and high-beam-quality photonic-crystal surface-emitting lasers: a tutorial (optica.org) ↩︎

6. General recipe to realize photonic-crystal surface-emitting lasers with 100-W-to-1-kW single-mode operation | Nature Communications ↩︎

7. Monolithically integrated photonic crystal surface emitters on silicon with a vortex beam by using bound states in the continuum (optica.org) ↩︎

8. GaN-based surface-emitting laser with two-dimensional photonic crystal acting as distributed-feedback grating and optical cladding | Applied Physics Letters | AIP Publishing ↩︎

9. Large area photonic crystal quantum cascade laser with 5 W surface-emitting power (optica.org) ↩︎

10. Wide-bandgap GaN-based watt-class photonic-crystal lasers | Communications Materials (nature.com) ↩︎

11. Emission Characteristics and Performance Comparison of Polyfluorene Lasers with One‐ and Two‐Dimensional Distributed Feedback - Heliotis - 2004 - Advanced Functional Materials - Wiley Online Library ↩︎